In Berlin gibt es eine Grundschulempfehlung – im übrigen erst nach der Klasse 6, da die Grundschule erst dann endet – die für das Gymnasium bei einem Notendurchschnitt besser als 2,2 erteilt wird. Falls die Eltern es wünschen – also bei einem Schnitt schlechter als 2,2 – gibt es ein Eignungsfeststellungsverfahren. Bei diesem Test sind in diesem Jahr 97 % der Teilnehmer durchgefallen.
Die Erziehungsberechtigten melden ihr Kind in dem von der Schulaufsichtsbehörde festgesetzten Anmeldezeitraum unter Vorlage des von der besuchten Schule ausgegebenen Vordrucks bei der als Erstwunsch benannten Schule an. Überschreitet die Notensumme der Förderprognose gemäß § 24 Absatz 2 Satz 6 der Grundschulverordnung den Zahlenwert 14, wird die Bewerbung nur dann in das Aufnahmeverfahren eines als Erst-, Zweit- oder Drittwunschschule gewählten Gymnasiums einbezogen, wenn die Eignung für den Besuch des Gymnasiums durch die erfolgreiche Teilnahme an einem Eignungsfeststellungsverfahren gemäß § 29a Absatz 2 bis 5 nachgewiesen wurde.
https://gesetze.berlin.de/bsbe/document/jlr-SekIVBE2010pG10
Schauen wir uns den Mathematikteil genauer an. Zu beachten ist – ich schrieb es eingangs bereits – dass die Kinder in Berlin sechs Jahre zur Grundschule gehen.
Bruchrechnung
Aufgabe 1 erfordert Grundkenntnisse in der Bruchrechnung: Erkennen und Eintragen von Brüchen am Zahlenstrahl, Darstellung einiger Bruchteile vom Ganzen, Erweitern
1 Brüche und ihre Darstellungen
a) Welche der Brüche [math]\frac{3}{4}[/math] [math]\frac{4}{3}[/math] [math]\frac{1}{3}[/math] [math]\frac{1}{6}[/math] [math]\frac{5}{4}[/math] [math]\frac{1}{2}[/math]sind auf dem Zahlenstrahl markiert? Trage nur die passenden Brüche ein.
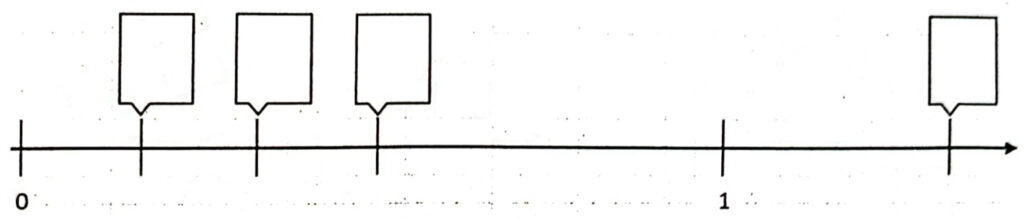
b) Zwischen [math]\frac{2}{5}[/math] und [math]\frac{3}{5}[/math] gibt es weitere Brüche. Trage zwei dieser Brüche am Zahlenstrahl ein und benenne sie.

c) Stelle [math]\frac{3}{4}[/math] im Rechteck dar.
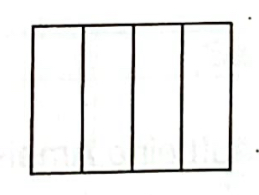
Welchen Bruch erhältst du, wenn du [math]\frac{3}{4}[/math] mit 3 erweiterst? Gib den erweiterten Bruch an und stelle ihn im Rechteck dar.
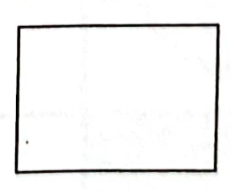
Es handelt sich um wirklich einfache Aufgaben aus der Einführungsphase in die Bruchrechnung. Umfangreiche Aufgaben zu Erweitern und Kürzen oder zu den Grundrechenarten kommen gar nicht vor.
Stereometrie
In der zweiten Aufgabe geht es vornehmlich um räumliches Vorstellungsvermögen.
2 Körper und ihre Netze
a) Welche Abbildungen sind keine Würfelnetze? Kreuze an.
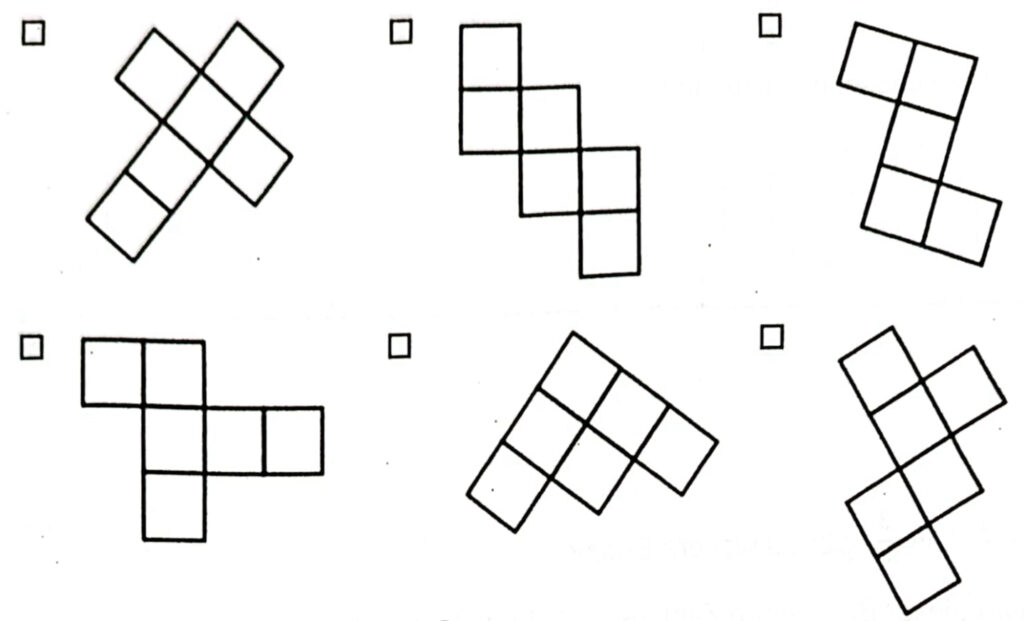
b) Elif sagt: „Ein Würfel ist auch ein Quader.“ Was denkst du?
Kreuze die richtige Begründung an.
- Elif hat nicht recht, denn ein Würfel hat gleich lange Kanten, ein Quader nicht.
- Elif hat recht, weil ein Würfel fast so groß wie ein Quader ist.
- Elif hat recht, denn ein Würfel ist ein Quader mit gleich langen Kanten.
c) In einem Quader läuft eine Ameise über die Seiten von Ecke zu Ecke. Ihr Weg ist mit Pfeilen markiert. Trage den Weg der Ameise in das Quadernetz ein.
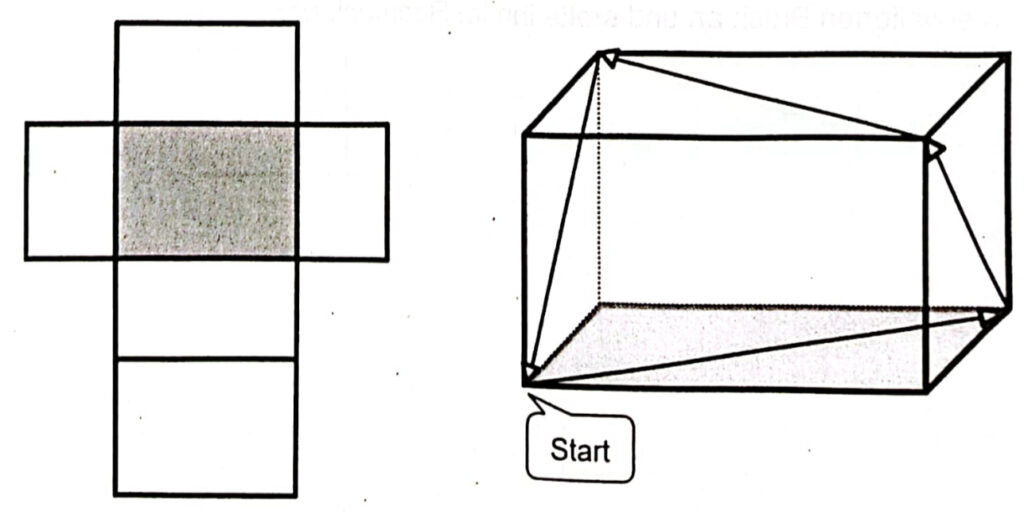
Bei der räumlichen Vorstellung scheiden sich die Geister. Hier haben manche Kinder große Schwierigkeiten. Dennoch sind diese Aufgaben nicht schwer und durchaus lösbar.
Stochastik
Es folgen Aufgaben zur Wahrscheinlichkeit. Die zentrale Idee ist das Säckchen mit verschiedenfarbigen Kugeln – ein Klassiker.
3 Wahrscheinlichkeit und Zufall
a) In den drei Säckchen befinden sich schwarze und weiße Kugeln – aber jeweils jeweils verschieden viele.
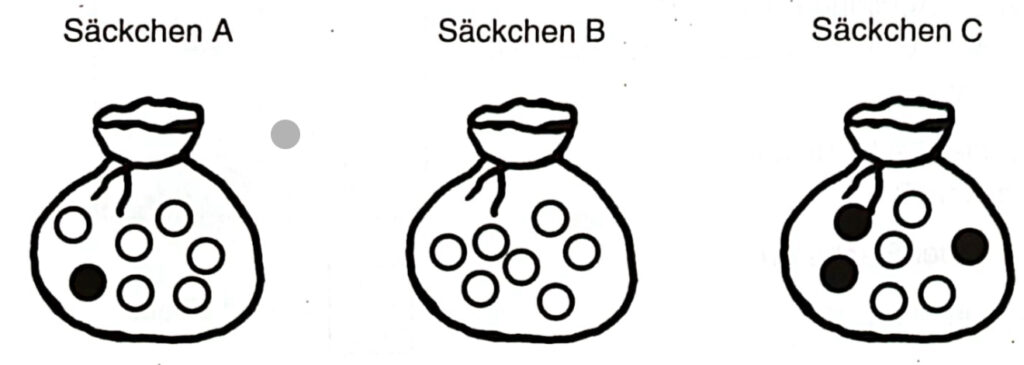
Welche Aussage passt zu welchem Säckchen? Es können auch mehrere Säckchen passend sein. Ordne zu.
| Aussage | Säckchen |
| Es ist unmöglich, eine schwarze Kugel zu ziehen. | |
| Es ist möglich, eine schwarze Kugel zu ziehen. | |
| Es ist fast sicher, eine weiße Kugel zu ziehen. |
b) Welche Anzahl von weißen und schwarzen Kugeln können in dem Säckchen sein, wenn die Aussage richtig ist? Zeichne eine Möglichkeit in das Säckchen.
| Aussage | Säckchen |
| Die Chance, eine schwarze Kugel zu ziehen, ist größer als die Chance, eine weiße Kugel zu ziehen. |  |
Naja, eine rein phänomenologische Betrachtung soll reichen… Die Aufgaben sind so leicht gestellt, dass auch Schüler, die noch nie etwas über Wahrscheinlichkeiten gehört haben, diese Aufgabe lösen können sollten.
Anwendungsaufgabe Schwimmbad Teil 1
In der nun folgenden Aufgabe geht es um die Anwendung der Mathematik in der Praxis. Es sind zwei Schwerpunkte: die Berechnung von Flächeninhalten und die Interpretation von Graphen im Koordinatensystem.
4 Mathematik im Schwimmbad
In einem Schwimmbad gibt es drei verschiedene Schwimmbecken.
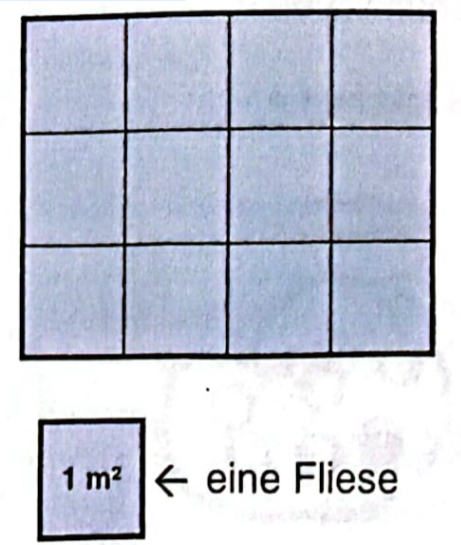
a) Du siehst in der Abbildung das erste Schwimmbecken von oben. Eine Fliese hat eine Größe von 1 m2. Wie groß ist die Fläche dieses Schwimmbeckens? Gib die Größe der Fläche an. Ergänze den Antwortsatz.
Das Schwimmbecken ist _______ m2 groß.
b) Hier siehst du das zweite Schwimmbecken von oben. Wie groß ist die Fläche dieses Schwimmbeckens? Gib die Größe der Fläche an. Denke an die Einheit.
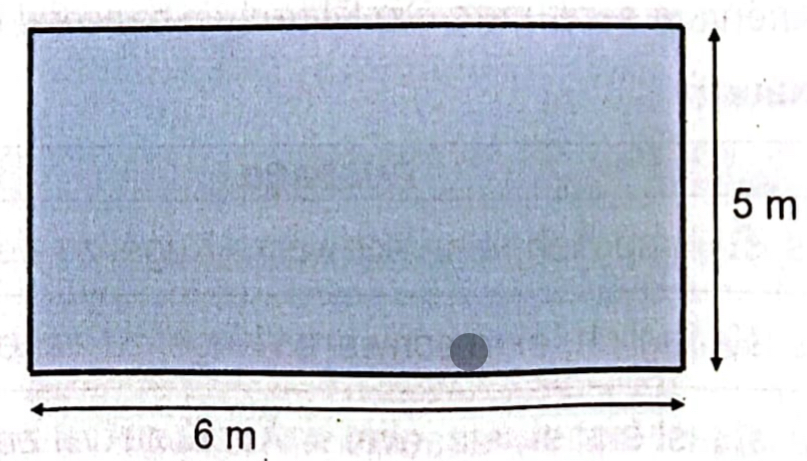
c) In dieser Abbildung siehst du das dritte Schwimmbecken von oben. Wie groß ist die Fläche dieses Schwimmbeckens? Notiere deinen Lösungsweg. Ergänze den Antwortsatz.
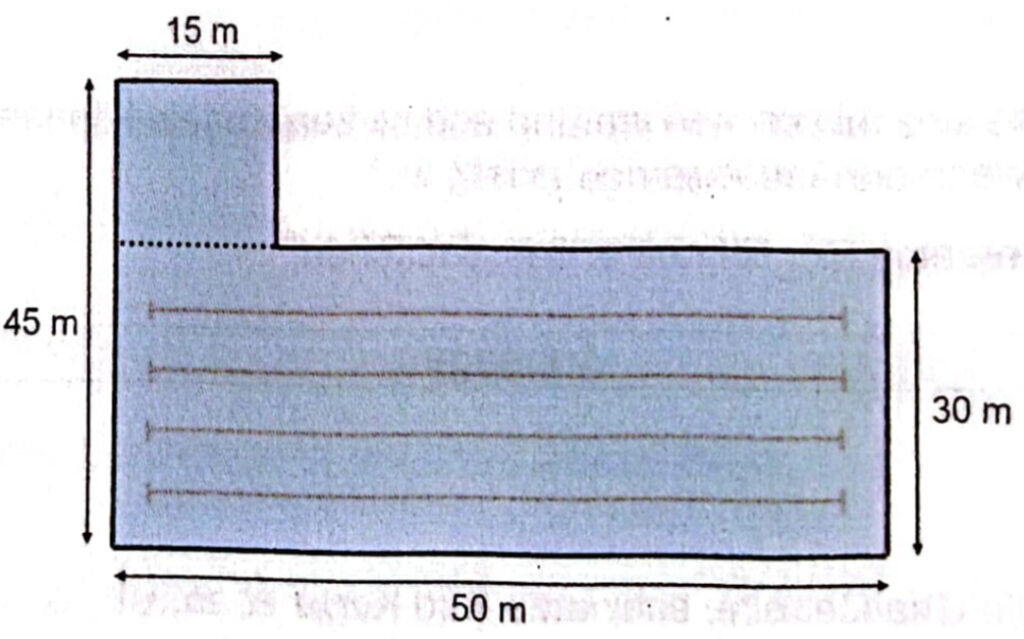
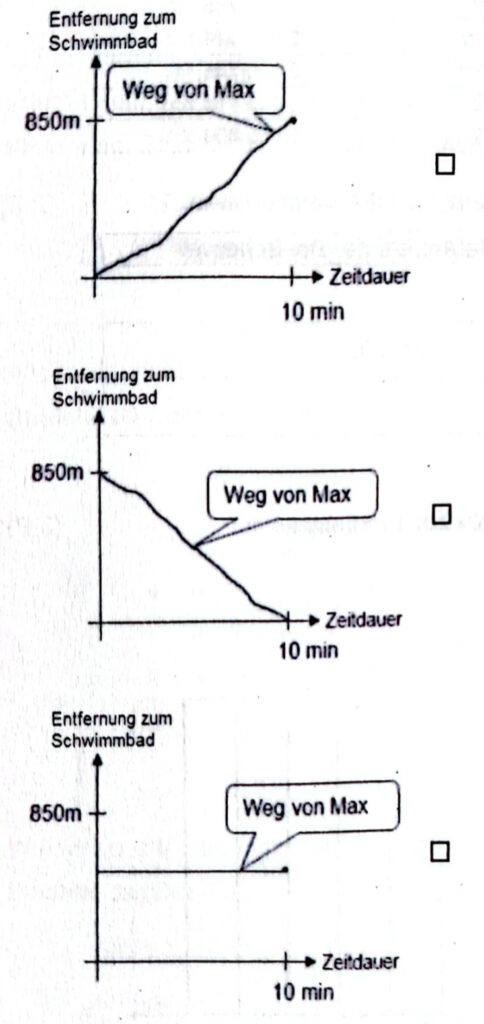
d) Max wohnt in der Nähe des Schwimmbads. Das Schwimmbad ist nur 850 Meter entfernt. Dafür braucht er zu Fuß 10 Minuten. Welches Diagramm zeigt den Weg von Max von zu Hause bis zum Schwimmbad? Kreuze an.
Dieses Diagramm habe ich gewählt, weil …
…. der Weg von Max zum Schwimmbad immer geradeaus geht.
…. die Entfernung zum Schwimmbad von 0 Meter auf 850 Meter steigt.
…. die Entfernung von Max zum Schwimmbad immer weniger wird.
Viel Text, wenig Mathematik! Ohne Worte… Scheitern die Kinder am Textverständnis oder an der Mathematik?
Anwendungsaufgabe Schwimmbad Teil 2
Im zweiten Teil der Anwendungsaufgabe geht es um einfachste Auswertungen zu den Besucherzahlen.
5 Anzahl der Besucher im Schwimmbad
In den letzten drei Jahren haben viele Menschen die Schwimmbäder in Berlin besucht. In der Tabelle siehst du die Anzahl der Besucher.
| Jahr | Besucher |
| 2018 | 6 766 112 |
| 2019 | 6 343 785 |
| 2020 | 3 036 111 |
| 2021 | 3 116 741 |
| 2022 | 5 113 168 |
| 2023 | 5 688 059 |
a) Runde die Zahlen für die Jahre 2021 und 2023 auf die Millionenstelle.
| Jahr | gerundete Anzahl der Besucher |
| 2021 | |
| 2022 | 5 000 000 |
| 2023 |
b) Ergänze die fehlende Säule für das Jahr 2020 im Diagramm.
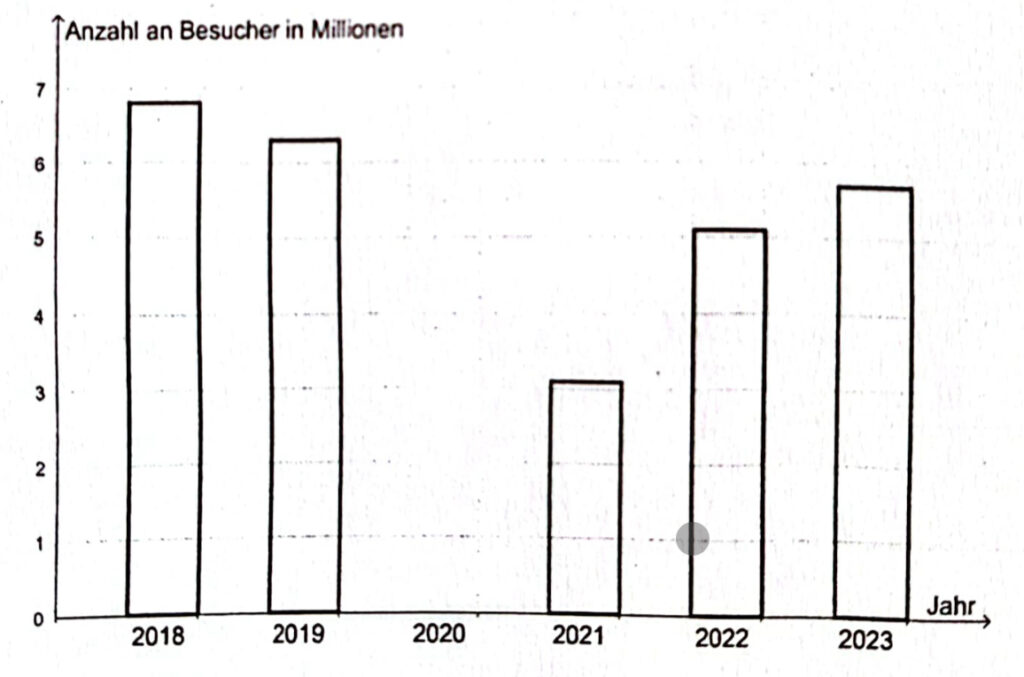
Ist die Behauptung richtig oder falsch? Kreuze an.
| Behauptung | richtig | falsch |
| Die Spannweite1 der Anzahl der Besucher beträgt etwa 4 Millionen Menschen. | ||
| Im Jahr 2019 haben etwa dreimal so viele Menschen die Schwimmbäder besucht wie im Jahr 2021. |
1 Die Spannweite ist die Differenz zwischen dem kleinsten Wert und größten Wert der Anzahl der
Besucher.
Erneut viel Text und kaum Mathematik. …und meine „Lieblingsaufgabe“ ist auch wieder dabei: Ankreuzen.
Terme und Gleichungen
6 Terme und Gleichungen
Terme können als Bild aus Punkten dargestellt werden. Zwei Beispiele siehst du hier:
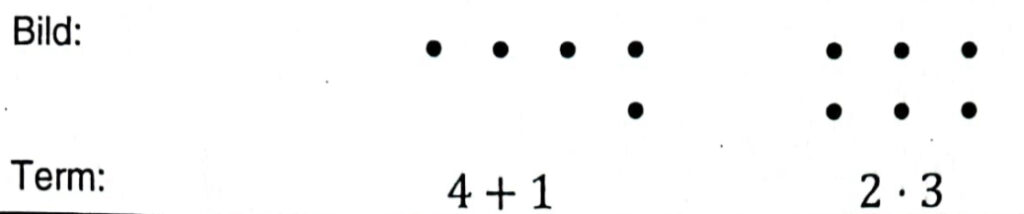
a) Welche Terme passen zu dem Bild? Kreuze an. Es sind auch mehrere Kreuze möglich.

b) Wie muss das Bild geändert werden, damit es zu dem Term passt? Streiche oder ergänze Punkte.

c) Wie wird das Muster fortgesetzt? Zeichne das Bild 4.
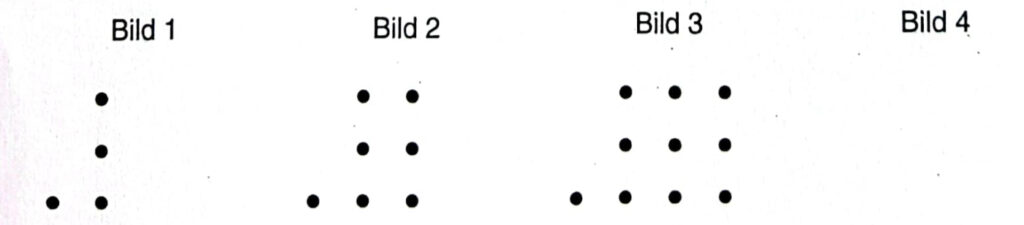
Welcher Term passt zu dem Bild? Notiere jeweils den Term. (Hinweis: Bild 17 ist nicht dargestellt.)
| Bild | Term |
| Bild 3 | |
| Bild 17 |
Ich habe ja grundsätzlich nichts gegen derart Logikaufgaben. Aber in einem solchen Test? Übrigens: Warum ist die Aufgabe mit „Terme und Gleichungen“ betitelt?
Sehen wir einmal davon ab, dass dieser Test die Eignung in Mathematik für das Gymnasium ab Klasse 7 nachträglich feststellen soll – was meiner Meinung nach ganz sicher so nicht geht – treibt mich eine viel spannendere Frage um:
Wie hätten all diejenigen abgeschnitten, die über den passenden Notendurchschnitt am Gymnasium gelandet sind? Vielleicht wären ja auch 97 % durchgefallen, man weiß es nicht…
Views: 73


[…] 97 % durchgefallen Wir haben unser Bildungssystem selbst kaputt gemacht Das Scheitern der Grundschule […]