Ich möchte eine Einschätzung zur ZP10 Mathe 2025 hinsichtlich der dort geforderten Schwierigkeiten abgeben.
Da die Unterlagen zur Prüfung nur für den dienstlichen Gebrauch bestimmt sind, veröffentliche ich hier nur Ausschnitte.
Prüfungsteil 1
Der Prüfungsteil 1 wird ohne Hilfsmittel (Taschenrechner, Formelsammlung) bearbeitet. Geprüft werden sollen ein Grundverständnis der Mathematik und das solide Beherrschen von Basisaufgaben.
In Aufgabe 1 ging es um Arithmetik, so z. B. das Umwandeln aus der Exponentenschreibweise in eine ganze Zahl oder das Berechnen einer Potenz. Es hätten statt drei (eine Wurzel musste auch noch gezogen werden) auch ein paar mehr Aufgaben sein dürfen.
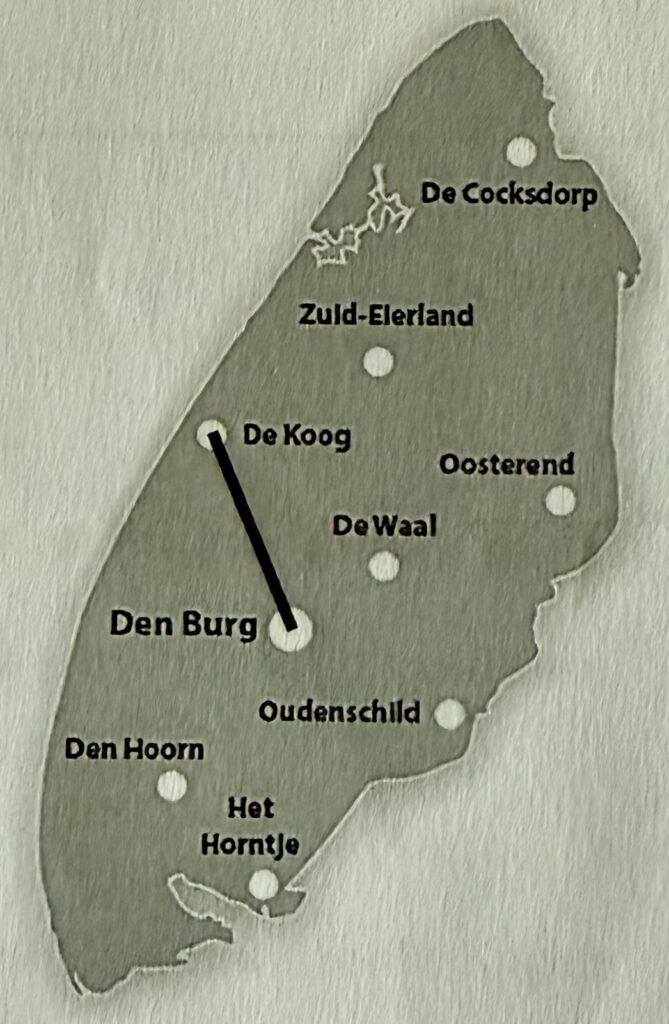
In Aufgabe 2 sollen die Schüler die N-S-Ausdehnung der Insel Texel anhand einer gegebenen Entfernung bestimmen und ihr Vorgehen beschreiben. Was das hier zu suchen hat, erschließt sich mir nicht.
Aufgabe 3 ist für meine Begriffe hier sehr gut platziert.
Zum einen muss gerechnet werden, zum anderen sollen die Schüler aber auch einen Zusammenhang als Term darstellen.
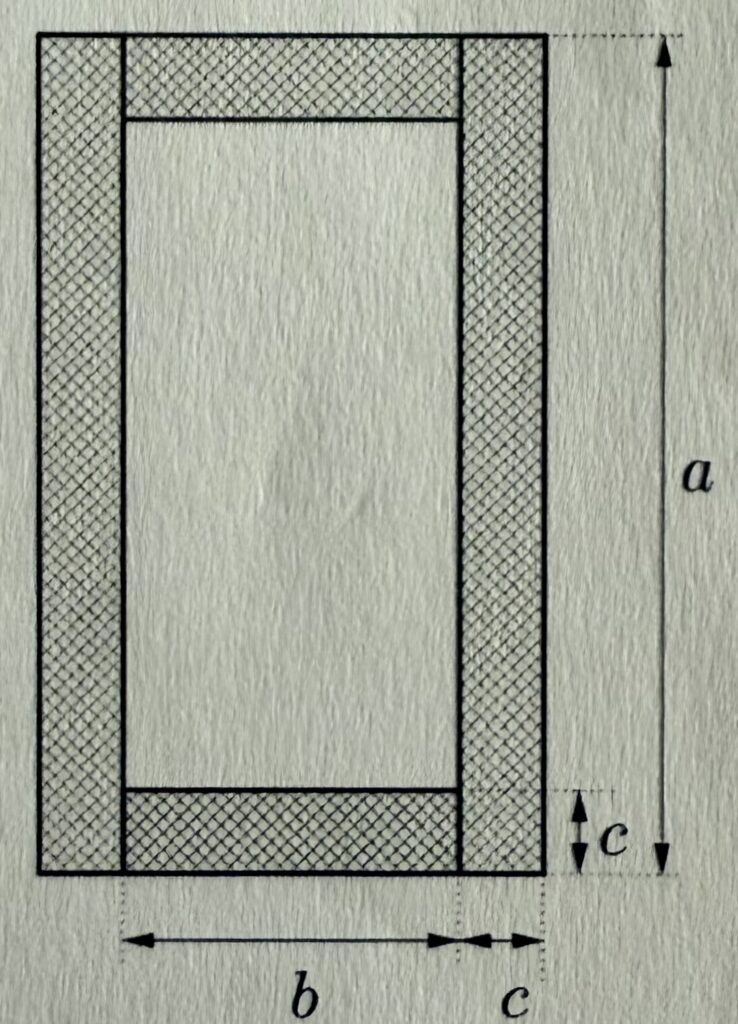
Auch die Aufgabe 4 ist gut gewählt: Punktprobe und Einzeichnen eines Graphen (lineare Funktion) in ein Koordinatensystem. Man hätte mehr herausholen können, bspw. die Nullstellen oder den Schnittpunkt beider Geraden zu berechnen.
Die Aufgabe 5 prüft kurz und knapp die Fertigkeiten der Schüler bezüglich der Wahrscheinlichkeitsrechnung. Allerdings halte ich Aufgabenstellungen – und das zieht sich durch die gesamte Prüfung – die das Ergebnis vorwegnehmen, um es danach zu überprüfen, für sinnlos, vor allem dann, wenn mit dem berechneten Wert nicht weitergearbeitet werden muss. Teilaufgabe b ist dann ein zweistufiges Zufallsexperiment, das sich mittels Baumdiagramm lösen lässt. Es geht übrigens wie so oft um verschiedenfarbige Kugeln, die gezogen werden müssen. Kleine Zusatzschwierigkeit: ohne Zurücklegen 🤔.
Zum Schluss wird in Aufgabe 6 das Lösen einer linearen Gleichung verlangt. Naja – die Steigung ist ein gemeiner Bruch, womit die Höchstschwierigkeit hier bereits benannt ist. Wo sind eine quadratische Gleichung, ein lineares Gleichungssystem oder eine Exponentialgleichung?
Alles in allem ist Teil 1 ein ein wohlwollend gemeinter Einstieg in die Prüfung mit einem akzeptablen Anteil an „echter“ Mathematik.
ZP10 Mathe 2025 – eine Einschätzung: Teil 2
Der Teil zwei besteht aus drei Aufgaben, die nun unter Zuhilfenahme von Taschenrechner und Formelsammlung gelöst werden dürfen.
Wie oben bereits bereits beschrieben, werden die Ergebnisse vorweggenommen. Die Schüler sollen zeigen, dass diese Lösungen korrekt sind. Das lässt mich ratlos zurück!
Aufgabe 1
Stellen Sie sich einen Luftballon vor, dessen Umfang an der dicksten Stelle gegeben ist. Zu berechnen – ach nein – zu überprüfen ist die Länge des Radius‘. Es geht direkt so weiter: Vorgegeben wird, dass man das Volumen des Luftballons über eine Kugel mit dem gegebenen Radius abschätzen kann. Erneut sollen die Schüler das bereits gegebene Resultat der Rechnung bestätigen.
Kleiner Einschub: Mir kommt das vor, wie ein Lehrer beim Arzt. Der lässt sich nämlich auch die bereits gestellte Selbstdiagnose nur noch bestätigen.
Jetzt wird es physikalisch – wow!
Angelehnt an das Archimedische Prinzip wird über das Steigen des Flüssigkeitsstandes in einem zylindrischen Becher das Volumen des Ballons ermittelt.
Der Ballon verdrängt dabei die Wassermenge, die seinem Volumen entspricht.
Leider ist das nicht ganz korrekt, da der Ballon ein klein wenig komprimiert wird, aber wir wollen mal nicht päpstlicher als der Papst sein.
Auch hier wieder:
Zeige dass der Luftballon ein Volumen von ca. 3 020 cm3 hat.
Ein wenig Prozentrechnung zur Abweichung zwischen Schätzwert und tatsächlichem Volumen zum Schluss, damit ist die Aufgabe fast erledigt.
Was jetzt folgt, hat in der Form hier nichts zu suchen (analog zur Texel-Aufgabe). Luftballons sollen in einem Pappkarton gestapelt werden.
Wenn ich den Rauminhalt des Kartons durch das Volumen eines Ballons teile, weiß ich genau, wie viele Ballons ich brauche.
Das Potential dieser Aufgabe ist riesig, was soll aber gemacht werden? Was heißt in diesem Zusammenhang „begründet“?
Entscheide begründet, ob die Berechnung zu viele oder zu wenige Ballons ergibt.
Aufgabe 2
Ach ja, die Bienen. Ein fleißiges Volk…
Alles dreht sich um die graphische Darstellung zur Anzahl der Bienenvölker in Deutschland zwischen 2007 und 2022.
Achtung Spoiler: Die Darstellung ist getürkt. Oder wurden schlicht die falschen Werte abgelesen? Peinlich – so oder so!
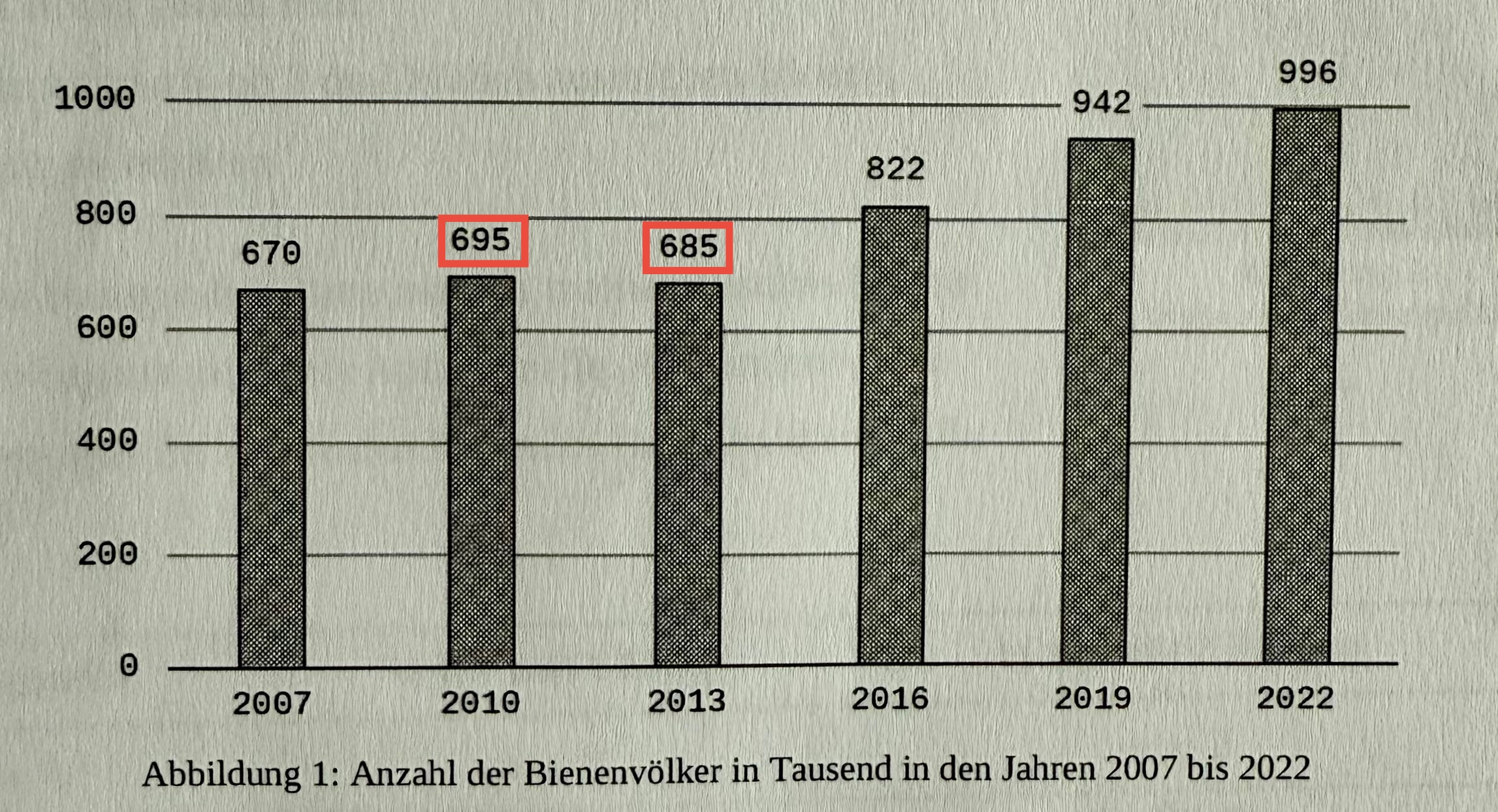
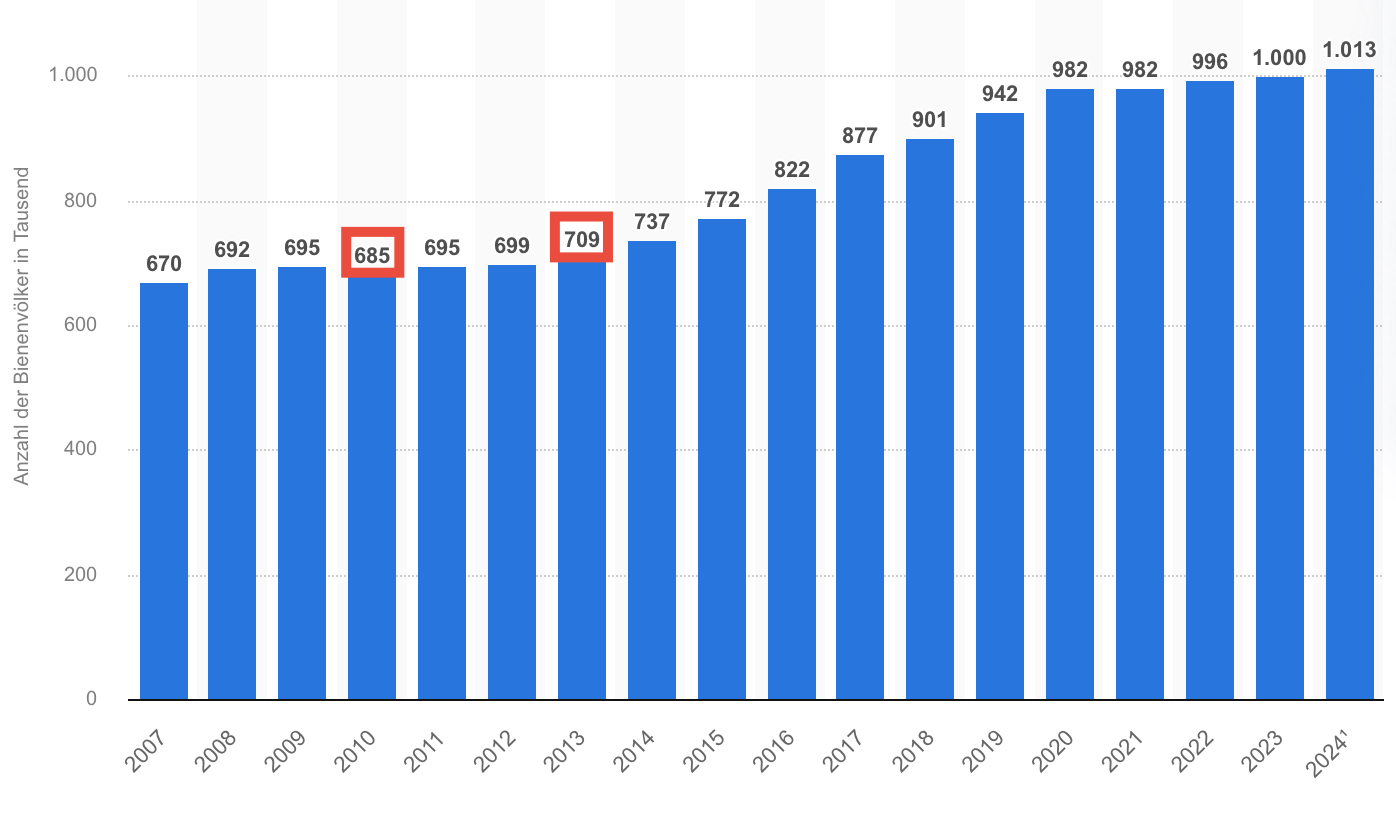
Was dann kommt, hat mit Mathematik so wenig zu tun, wie eine Kuh Eier legen kann: Checklisten.
Warum?
Wenn man nur zwei Auswahlmöglichkeiten hat, ist die Chance richtig zu liegen, bei 50 %. Da keine Begründung verlangt wird, kann keiner nachvollziehen, warum der Schüler die Lösung wählt. Das mag mit Blick auf das Ergebnis der Prüfung nachrangig sein, ist aber für eine solide Auswertung untauglich.
Bullshit-Mathematik, oder besser: gar keine Mathematik!
Anschließend ist zu begründen ob die Zunahme von 2016 auf 2019 nahezu genau so groß ist wie die von 2019 auf 2022. Ich frage mich erneut, was in diesem Zusammenhang „begründet“ heißt? Phänomenologisch, rechnerisch, zeichnerisch oder was auch immer?
Die nachfolgende Aufgabe will prüfen, ob die Schüler in der Lage sind, mehrstufig zu rechnen. Aus der Zahl der Zellen pro Wabe und der Füllmenge soll ermittelt werden, ob 3 dm2 Waben ausreichen, um ein Kilogramm Honig zu erhalten.
Die Aufgabe ist grundsätzlich gut, aber Prüfungsniveau in einer 10?
Weiter geht’s mit der Wabenstruktur und ihrem Aufbau.
Den Aufbau von Honigwaben kann man als mathematisches Muster betrachten.
Aha… Wie wäre es mit „regelmäßige Sechsecke“? Okay, etwas später fällt das Wort „sechseckig“ dann doch. Aber weiter im Text.
Die Begründung, dass die Anzahl nicht linear wächst, ist ziemlich leicht. Allerdings wird auch hier auf eine mathematische Herangehensweise verzichtet. Der Funktionsbegriff taucht an keiner Stelle auf. Beschreibendes Begründen oder so…
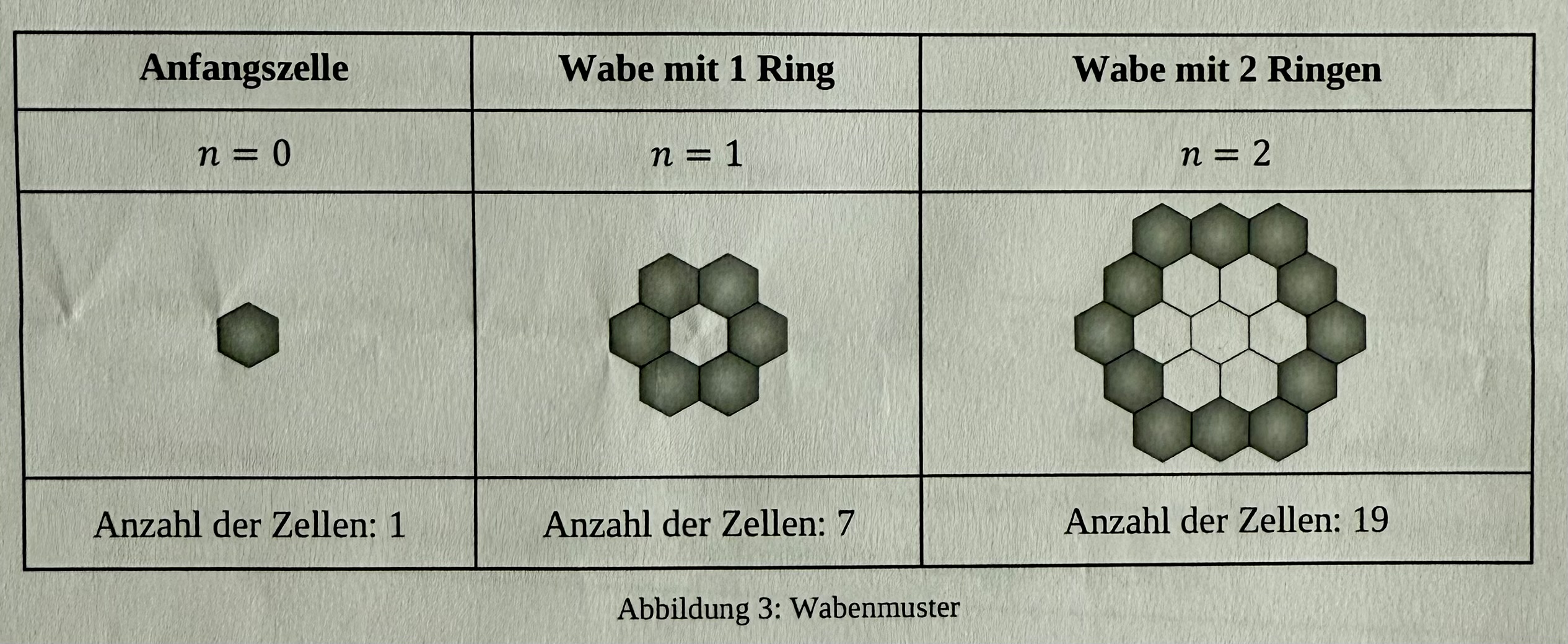
Was folgt, ist eine explizite Zuordnungsvorschrift zur Ermittlung der Gesamtzahl der Waben in Abhängigkeit von der Anzahl der Ringe:
sn = 1 + 3n + 3n2
Die folgende Aufgabe (Berechnung für n = 3 Ringe) ist trivial. Komplizierter wird es danach, wenn es darum geht, die Anzahl der Waben des sechsten Ringes zu ermitteln. Hier ist genaues Lesen der Aufgabenstellung gefragt.
Der Knüller ist Aufgabe g).
Bestimme, aus wie vielen Ringen eine Wabe mit 217 Zellen besteht.
Ich würde hier die obige Gleichung nehmen und bezogen auf n lösen. Die Lehrerhandreichung begnügt sich mit systematischem Probieren. Bullshit-Mathematik zum Zweiten.
ZP10 Mathe 2025 – eine Einschätzung: Aufgabe 3
Grundsätzlich handelt es sich hier um die anspruchsvollste Aufgabe, Sie wittern bereits das „ABER“, richtig?
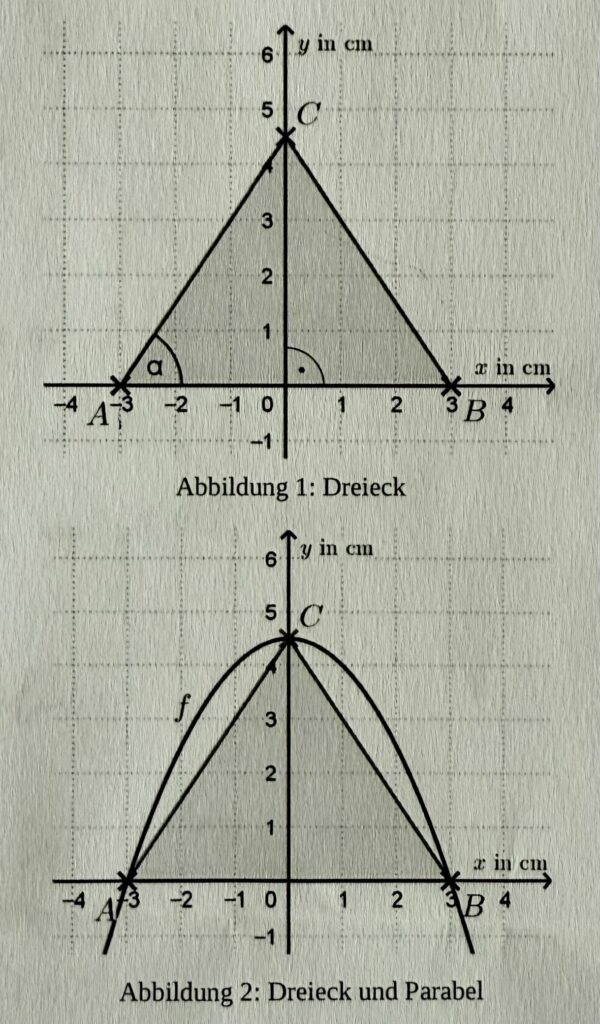
Zu berechnen sind Flächeninhalt, Umfang des Dreieckes sowie die Größe des Winkels α. Geprüft werden Kenntnisse zu Pythagoras und Trigometrie.
Im zweiten Schritt wird nun die Parabel eingezeichnet.
Ich frage mich jetzt, wie ein Schüler der Klasse 10 begründen soll, dass die Gleichung
f(x) = a(x + 3)(x – 3)
unter der Annahme, dass a < 0 sein muss, zum Graph passt. a < 0 bedeutet „nach unten geöffnet“ – das ist lösbar, aber die Linearfaktorzerlegung schießt über das Ziel hinaus. Wenn ein Schüler nicht mit Blindheit geschlagen ist, dürfte er zumindest sehen dass die Nullstellen etwas damit zu tun haben. Aber was ist mit dem mathematischen Verständnis?
Die Bestimmung des Faktors a wird aus für mich unerfindlichen Gründen angeleitet:
Bestimme den Wert des Faktors a mit Hilfe des Punktes C.
Es folgen – wie soll es anders sein – Ankreuzaufgaben. Bullshit-Mathematik zum Dritten.
Abschließend sollen die Koordinaten von C derart bestimmt werden, dass das Dreieck rechtwinklig ist. Welchen Lösungsansatz sollen die Schüler hier finden? Mir fällt hier direkt der Satz des Thales ein – den Prüflingen auch?
Fazit
Dreimal (oder öfter) Bullshit-Mathematik. Ich bitte wegen der Wortwahl um Entschuldigung!
Kein Gleichungssystem, keine quadratische oder Exponentialgleichung, keinerlei technische Anwendung oder Betrachtung von Wachstumsprozessen, die linearen Funktionen werden nur ein wenig angeschnitten.
Wieso muss man Ergebnisse vorgeben, um sie zu prüfen. Das widerspricht dem Grundgedanken der Mathematik! Was haben Checklisten in einer Prüfung zu suchen? Wieso wird eine offizielle Statistik falsch wiedergegeben?
Und vor allem: Warum ist eine Mathematikprüfung derart sprachlastig?
Views: 25

